제5장 산포도 (범위, 사분위수 범위, 분산, 표준편차, 변이계수, 비대칭도, 첨도)

<학습개요>
데이터(변수)의 중심위치나 집중경향을 나타내는 대표값과 함께 집단의 변이(변동) 정도를 나타내는 통계적 수치를 산포도라고 하며, 산포도의 통계량에는 범위ㆍ사분위수범위ㆍ분산ㆍ표준편차ㆍ변이계수ㆍ비대칭도ㆍ첨도 등이 있다. 산포도의 통계량에 가운데 분산과 표준편차가 가장 널리 사용된다. 변이계수를 통해 측정단위가 다른 변수들의 산포도를 비교할 수 있고, 데이터의 분포 형태는 비대칭도와 첨도를 통해 확인할 수 있다.
| ○ 산포도(measures of dispersion) - 데이터의 관찰값들이 흩어져 있는 정도 • 집단을 구성하는 개체들의 변이(=변동)정도를 통계적 수치로 나타내는 통계량 - 산포도를 나타내는 통계량 • 절대산포도 : 범위, 사분위범위, 분산, 표준편차 • 비교산포도 : 변이계수 • 분포의 형태: 비대칭도, 첨도 |
5.1 범위와 사분위수범위
가. 범위(R, Range) :


‧데이터 (변수 )의 가장 큰 관찰값 (최대값 )에서 가장 작은 관찰값 (최소값최소값)을 뺀 것으로 최대값과 최소값 사이의 거리
‧데이터의 변이(변동) 정도를 가장 간단하게 파악할 수 있다.
‧일중 최고․최저 온도의 차이, 농산물 품질의 균일도 등의 표현에 적합
나. 사분위수범위(interquartile range, IQR)
‧ 전체 데이터를 순서대로 정리하여 4등분한 후 데이터의 가운데 위치한 50% 부분에 대해 범위를 구한 것이다. 그 중 첫째를 제1사분위수( Q1 ), 둘째를 제2사분위수( Q2 ), 셋째를 제3사분위수( Q3 )라 한다.
‧ 제3사분위수와 제1사분위수의 차를 사분위범위라 한다.

‧데이터를 크기 순서로 정돈해서
개로 나누었을 때 각 위치에 해당하는 관찰값을
분위수라고 한다.
‧
k 가 100이면 백분위수, k가 10이면 십분위수, k가 4이면 사분위수라고 부른다.
‧사분위수는 제일 작은 관찰값에서부터 25%, 50%, 75%에 해당하는 관찰값을 각각 제1사분위수(
, 25백분위수), 제2사분위수(
, 50백분위수), 제3사분위수(
, 75백분위수)라고 하는데, 제2사분위수는 데이터의 가운데 위치하므로 중앙값과 일치한다. ‧

= : 제3사분위수와 제1사분위수 사이의 거리를 나타낸다.
‧사분위수범위는 데이터의 중앙값을 중심으로 가운데 부분을 이루고 있는 50%의 관찰값들이 얼마나 넓은 범위에 흩어져 있는지를 나타내는 산포도의 통계량을 나타낸다.
‧특이값의 영향을 받지 않는 장점이 있으나 데이터 전체의 산포도를 설명하지는 못한다.

5.2 분산과 표준편차
○분산(variance)
산술평균에산술평균에대한 편차의 제곱을제곱을모두 합하여 관찰값의관찰값의개수 (개체수,n) 로 나누어 준 값
자료가 평균을 중심으로중심으로얼마나 광범위하게 분포하고분포하고있는가를 나타내는 통계량
○표준편차 (standard deviation)
분산의 제곱근
○산술평균에 대한 편차는 평균과 관찰값 사이의 거리이고, 편차를 토대로 하는 분산과 표준편차는 산술평균을 중심으로 관찰값들이 어떻게 분포하는지를 보여주는 통계량이다.

○분산과 표준편차는 데이터가 평균을 중심으로 얼마나 광범위하게 분포하고 있는 가를 나타내는 통계량이다. 표준편차는 평균으로부터 관찰값까지의 평균거리라 생각할 수 있다. 분산은 관찰값과 평균의 차이를 구하여 각각을 제곱해 합한 후 데이터의 개수로 나누어 평균제곱을 구한 것이다. 표본분산계산에서 표본크기 n 대신 n-1로 나눌 때 모분산을 더 잘 추정하는 것으로 밝혀져 있다(자유도 df).
가. 표본분산
○ 관찰값들 간의 차이가 클수록 큰 값이 나온다
∴ 편차제곱합을 이용하는 분산과 표준편차가 산포도를 나타내는 통계량으로서 우수하다

나. 표본표준편차
○ 분산의 계산과정 중 편차제곱에 의해 측정단위가 변한다. 예컨대관찰값의 단위가 cm일 때 분산의 경우 cm
로 길이에서 면적으로 변한다.따라서 원래의 측정단위로 만들기 위해 분산의 제곱근을 취하는데 그렇게 해서 얻은 값이 표준편차이다.
○표본표준편차(standard deviation) 구하는 식:

다. 정의식과 계산식


라. 표준편차의 해석
○ 표준편차는 평균을 중심으로 ±1표준편차 범위, 즉
또는
범위가 전체 관찰값(개체)의 68.26%를 포함한다.(6장.정규분포 참조)
○ 표준편차가 클수록 관찰값들이 넓게 흩어져 있어 그 변수의 변이가 크다는 것을 의미한다.
○ 표준편차를 나타낼 때는 평균±표준편차로 쓰며, 표준편차의 소수점 이하 자릿수는 평균과 같게 한다.
○ 동일 변수의 평균이 같은 집단들은 표준편차의 크기를 가지고 그 집단의 특성을 비교할 수 있다.
마. 자유도와 불편추정량
○표본분산에서 편차제곱합을 자유도(degree of freedom,
)
-1로 나누어야 편의(bias)되지 않은 모분산을 얻을 수 있다. 자유도
-1로 나누어서 구한 표본분산을 모분산의 불편추정량이라고 한다.○표본분산에서 편차제곱합을 자유도(degree of freedom,
)
-1로 나누어야 편의(bias)되지 않은 모분산을 얻을 수 있다. 자유도
-1로 나누어서 구한 표본분산을 모분산의 불편추정량이라고 한다.
자유도 (df, Degree of Freedom)
| -모집단을 추론하는 표본에서 모집단의 특성을 나타내는 기술통계량을 산출할 때, 특정한 기술통계량을 제외하고 자유롭게 나타날수있는 데이터의 경우의 수를 말한다. -어떤 데이터가 100개라면 평균이라는 값으로 해당데이터 전체를 설명할 수 있다. 즉, 1개로 100개를 설명하게 된다는 의미가 된다.이때,평균은 데이터를 대표하는 값이 모두 100개의 데이터가 평균과 같다는 뜻은 아니다. 즉, 100개중 하나의 고정된(계산된)값으로 전체를 설명할 수있 기에 나머지 99개의 값은 평균값과 비슷하거나 다소차이가있는 값일 수 있다. 다시말해 나머지 99개의 값은 나름대로의 값을 취할 수 있는 경우의 수가 있다는 것이다. 해서, 100개로 이뤄진 데이터를 평균으로 설명한다면 자유도는 99개가 된다. -또한 30개 이상의 큰 표본의 경우에는 표본의 분산을 구할 때 굳이 자유도 (n-1)을 고려하지 않아도 된다. |
| -표본분산에서 편차제곱합을 n-1로 나누어야 편의 (bias) 되지 않은 모분산을 얻을 수 있다 . -자유도 n-1로 나누어서 구한 표본분산을 모분산의 불편추정량이라고 한다 . -모집단은 변하지 않는 상수이기 때문에 동일한 모집단에서 랜덤으로 추출한 크기 n의 표본 (확률표본 )은 관찰값이 변동된다 하더라도 표본평균의 기대값은 변화하지 않는다. |
5.3 변이계수(변동계수, coefficent of variation) :
○ 두 개 이상의 데이터에 대한 퍼짐 정도를 비교하기 위해서 두 데이터의 표준편차를 구하여 비교하는 것은 측정단위가 서로 다르거나 데이터값의 차이가 커서 무의미 한 경우가 많다. 이러한 경우에 사용하는 측도가 표준편차를 평균으로 나눈 변이계수이다
○ 절대산포도는 데이터(변수)의 측정단위가 다르거나 평균이 크게 차이 날 때는 변이(변동)를 직접 비교할 수 없다.
○ 이와 같은 경우 산포도의 상대적인 크기를 나타내는 비교산포도(comparative dispersion)로서 변이계수를 이용한다.
○ 측정단위가 다른 두 집단의 변이(변동)정도를 비교할 때 사용할 수 있는 이유는 단위가 없기 때문이다.
- 초장과 수량의 변이크기, 무게(kg)와 신장(m)의 변이크기 등을 비교할 때 이용.
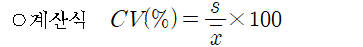

5.4 비대칭도와 첨도 → 분포의 모양
가. 비대칭도(skewness)
○관찰값들의 분포가 대칭적인지 비대칭적인지를 나타내는 통계량
○비대칭도의 데이터(변수)의 분포가 좌우 어느 쪽으로 치우쳐 있는지를 나타내는 수치로서 피어슨의 계수(Pearson’s coefficent, )를 이용한다. Sk는 식1 이나 식2 으로 구한다

나. 첨도(kurtosis)
○관찰값들이 대표값 주위에 얼마나 흩어져 있는지를 나타내는 통계량
○평균을 중심으로 분포의 정점이 얼마나 뽀족한지를 나타내는 수치로서 첨도의 적률계수를 이용한다.
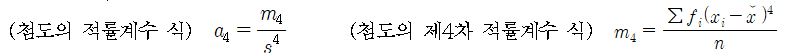

1. 비대칭도 Sk값이 (+)이면 오른쪽꼬리 분포를 보이고, Sk = 0일 때 정규분포하며 Sk값이 (-)이면 왼쪽꼬리분포이다
2. 첨도의 적률계수에 의한 분포모양. α4=3은 정상의 정규분포, α4>3이면 관찰값이 평균근처 밀집분포 보인다
<예제) 고소득층과 저소득층의 하루 일당에 대한 표준편차와 변동계수를 구하고, 상대적으로 두 자료집단의 흩어진 정도를 분석하여라. (단, 단위는 $이다.)
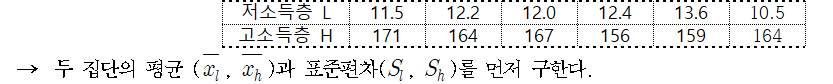

<정리하기>
1.산포도는 데이터(변수)가 흩어진 정도(변이, 변동)를 나타내는 통계량이다. 범위‧사분위수범위‧분산‧표준편차 등은 절대산포도이고, 변이계수는 비교산포도이며, 비대칭도와 첨도는 분포의 형태를 나타낸다.
2.범위는 최대값과 최소값 사이의 거리를 나타내며, 사분위수범위는 전체데이터의 가운데 50% 산포도를 나타낸다.
3.분산과 표준편차는 산포도를 가장 잘 나타내며 및 의 범위는 전체 관찰값의 68.26%를 포함한다.
4.변이계수는 산술평균에 대한 표준편차의 비로서 단위가 없어 측정단위가 다른 집단들의 변이 정도를 비교하는 통계량으로 적합하다.
5.비대칭도는 데이터의 분포가 대칭적인지 여부를 나타내며, 첨도는 관찰값들의 흩어짐 정도를 나타낸다.
'생물통계학' 카테고리의 다른 글
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 7. 표본분포 (8) | 2022.11.15 |
|---|---|
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 6. 확률분포 (9) | 2022.11.14 |
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 4. 대표값 (17) | 2022.11.12 |
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 3. 도수분포표와 그래프 (7) | 2022.11.12 |
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 2. 표본추출과 데이터 수집 (11) | 2022.11.11 |