7. 표본분포
<학습개요>
확률분포는 주로 모집단을 나타내는 확률변수에 관한 것이고, 표본분포는 표본통계량의 확률분포이다. 표본분포는 표본평균이나 표본분산 등을 확률변수로 하기 때문에 통계량과 모수의 관계를 규명해준다. 표본분포에는 평균의 표본분포, t-분포, x2-분포, F-분포 등이 있다
7.1 평균의 표본분포와 표준오차
| ○이항분포와 정규분포 등 확률분포는 주로 모집단을 나타내는 확률변수에 관한 것이다. 그러나 실제 모집단의 특성이나 분포는 거의 알지 못하며, 그걸 다 알기 위해서는 시간과 비용이 많이 들기 때문에 모집단의 일부인 표본의 통계량으로 모집단의 모수를 추측하게 된다. 표본의 통계량인 표본평균과 표본분산 등은 확률변수이고, 통계량을 확률변수로 하는 확률분포를 표본분포(sampling distribution)라고 한다. ○확률분포 -이항분포(Bionomial Distribution) : 실험결과가 두 가지로 나타나는 변수의 확률분포 -포아송분포(Poisson Distribution) : 희귀사건의 확률분포 -정규분포(Normal Distribution) : 좌우대칭인 종모양, 평균과 표준편차에 따라 곡선의 위치와 모양이 다르다. ○표본분포(sampling Distribution) - 이항분포‧포아송분포‧정규분포등은 대부분 모집단을 나타내는 확률변수에 관한 분포이다 . - 그러나, 모집단의 특성이나 분포는 파악하기 어렵고 , 조사에 시간과 비용이 많이 든다 . - 따라서 모집단의 일부인 표본의 통계량을 이용 모집단의 모수를 추측하게 되며 - 이 때, 표본의 통계량인 표본평균과 표본분산이 확률변수이고 , 통계량을 확률변수로 하는 확률분포를 표본분포라고 한다. - 표본분포의 이와 같은 특성은 통계량과 모수 간의 관계를 설명하므로 모수추정과 가설검정의 이론적 토대가 된다 . - 표본분포에는 평균의 표본분포, t–분포, x2–분포, F–분포 등이 있다. |
평균의 표본분포


에 가까워진다
○ 따라서 정규분포를 하지 않는 모집단에서도 표본평균들에 대해서는 정규분포를 이용하는 통계분석이 가능해진다.
모분산을 모르는 집단에서 단일표본을 추출하는 경우
○ 표본의 표준편차 (표준오차) s 만 구할 수 있다
○표준오차를 구하기 위해서는 같은 모집단에서 크기가
인 표본을 계속 추출하거나, 단일 표본에서

표준오차 이용

-표본평균을 표준화하여 얻은 Z값은 μ=0, σ=1인 정규분포를 따른다
.

- 따라서 표본평균에 대해서도 표준정규분포를 이용할 수 있다.
(예7-2) 1,000 개체로 이루어진 모집단의 평균이 68.2이고 표준편차가 2.5이다. 이 모집단에서 n=100인 하나의 표본을 취하는 경우 표본평균이 68.9보다 클 확률은?
→ 먼저, 표본평균 68.96를 표준단위로 바꾼 다음에 표준정규분포표에서 해당 면적을 찾아야 한다.
○ 평균의 표본분포는 정규분포하고 표준편차는 표본평균들의 산포도이다.
- 표준오차 : 표본평균들의 산포도
- 표준편차 : 집단 내 개별 관찰값들의 산포도
평균±표준오차의 유의숫자 표기
○평균은 표준오차를 3으로 나누어 소수점 이하 첫 자리부터 0이 아닌 수가 처음 나온 자릿수만큼 소수점 이하 자릿수를 부여한다.
○표준오차는 평균보다 한 자리 더 많은 자릿수를 쓴다.

7.2 t –분포


-정규분포를 따르는 모집단에서 크기가 n<30인 표본을 추출하고 표본평균의 편차를 표준오차 나누어 준 값을 t라 할 때, 통계량 t의 확률분포는 자유도 n – 1 인 t-분포를 따른다
○ t-분포표와 이용
- 자유도(df) : 9, 유의수준(α) : 0.05 일 때,
- <부표 5> t-분포표를 찾아 t0.05(9)=2.262로 쓴다.
→ t=-2.262보다 작을 때의 면적 0.025와 t= 2.262보다 클 때의 면적 0.025를 합한 것이 0.05라는 의미이다.
t–분포의 특성
○ t–분포는 정규분포와 상당히 비슷하게 생겼다.
○ t –분포는 평균을 중심으로 좌우대칭이고 종 모양이나, 정규분포보다 중앙이 낮고 양끝은 높다.

○
t–분포는 자유도(df)에 따라 분포모양이 달라진다.(df 클수록 정규분포에 가까워 진다)
○t–분포에는 반드시 자유도가 명시되어야 한다.
t–분포의 활용
○ 모분산이 알려져 있지 않은 경우 모평균의 신뢰구간을 추정하는 데 이용한다.(8장)
○ 미리 가정한 모평균이 표본평균과 같은지에 대한 귀무가설을 검정하는 데 이용한다.(9장)
○ 두 표본평균 간 차이를 검정하는 데 이용한다.(10장)
<예 7-4> 생후 100일 된 돼지의 평균 체중은 50kg으로 알려졌으나 분산이 얼마인지는 모른다. 목장에서 16마리를 랜덤으로 추출해서 체중을 측정한 결과 평균 58kg이고 분산 81이었다.생후 100일 된 돼지들 중에서 16마리를 반복적으로 추출하여 평균을 구했을 때 58kg보다 더 큰 돼지가 나올 확률은 얼마인가?
→ 모분산을 모르고, 𝑛=16으로 소표본이므로 t-분포를 이용한다
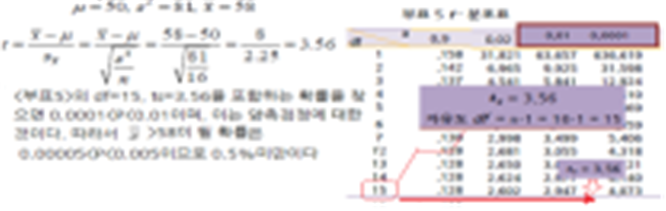
7.3 카이제곱 x-2-분포 : 표본분산의 분포

x2–분포표와 그 이용
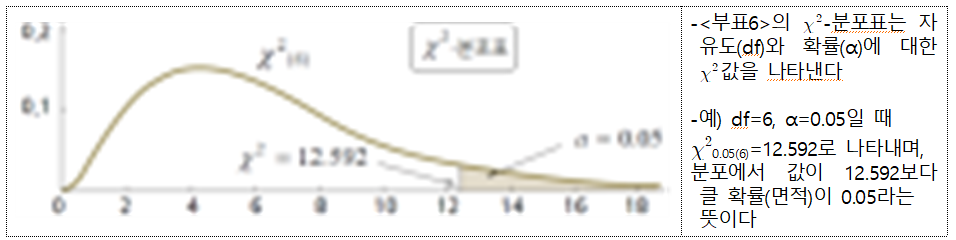
○ 표본분산의 분포로 모분산에 대한 신뢰구간을 구하는 데 이용한다.(추정,8장)
○ 모분산비가 표본분산비와 같은지를 검정하는 데 이용한다.(가설검정)
○ 정규분포의 적합성을 검정하거나, 특히 이산형 변수의 통계분석에 주로 이용된다.(15장)
※ x2이용에 대한 추가 설명
‧ 모분산비가 표본분산비와 같은지를 검정하는데 이용한다.
‧ 정규분포의 적합성을 검정하거나, 특히 이산형 변수의 통계분석에 주로 이용된다.
‧ 실제로 관찰된 빈도가 기대빈도와 얼마나 근접한지를 검정할 때 사용한다
‧ 주로 명목척도로 측정된 두 변수간의 상관관계를 검정할 때 사용함
‧ 표본분포로 자유도에 의해 구체적인 분포가 결정됨
7.4 f-분포
f-분포 특성

f–분포표와 이용

f-분포의 이용
○두 모집단의 분산이 같은지 여부를 판단함으로써 모분산의 가설검정을 하는 데 이용한다.
○분산분석(11장 참조)에 많이 사용된다. 비교집단이 3개 이상인 경우 사용됨


.
※ 부족하지만 글의 내용이 도움이 조금이라도 되셨다면, 단 1초만 부탁드려도 될까요? 로그인이 필요없는 하트♥(공감) 눌러서 블로그 운영에 힘을 부탁드립니다. 그럼 오늘도 행복한 하루 되십시오^^
'생물통계학' 카테고리의 다른 글
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 9. 가설검정 (7) | 2022.11.17 |
|---|---|
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 8. 모수추정 (10) | 2022.11.16 |
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 6. 확률분포 (9) | 2022.11.14 |
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 5. 산포도 (4) | 2022.11.14 |
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 4. 대표값 (17) | 2022.11.12 |