9. 가설검정
[학습개요]
가설검정은 추측통계에서 모수값을 미리 가정해 놓고 표본의 통계량이 가정한 모수와 일치하는지를 검정하는 통계적 절차를 말한다. 가설검정을 하는 이유는 모수와 통계량 간의 차이가 참인지 우연인지를 판정하기 위함이다. 통계적 가설은 ‘지금까지 알려진 것과 같은’ 귀무가설과 ‘새롭게 주장하는’ 대립가설이 있다.
9.1 가설검정의 개념 : 표본을 이용하여 모집단의 주장이 옳고 그름을 판정하는 과정
| 가설검정(hypothesis test) 추측통계에서 모수값을 미리 가정해 놓고 표본의 통계량이 가정한 모수와 일치하는지를 검정하는 통계적 절이며, 가설검정은 모수와 통계량 간의 차이가 참인지 우연인지를 판정하기 위함이다. 모수의 값으로 가정하는 것을 ‘가설을 세운다’고 말하며, 이 가설을 ‘통계적 가설’이라고 부른다. 가설검정에서 통계적 가설이 맞다고 판정되면 채택(accept)하고, 가설이 틀렸으면 기각(reject)한다 통계적 가설은 ‘새로운 주장’을 대립가설로, 그에 반대되는 주장을 귀무가설로 한다. |

가. 귀무가설과 대립가설 : 연구자가 어떤 현상에 대해 “그럴 것이다”라고 추측하는 부분으로 모집단에 대한 추정이 된다.
① 귀무가설(h0) : 지금까지 알려진 것과 같다. 검증의 대상이 된다
-표본에서 추정한 모평균이 지금까지 알려진 모수값과 같다는 주장을 하기 때문에 차이가 없다는 것을 강조하는 뜻에서 ‘귀무’라는 용어를 쓴다.
② 대립가설(H1) : 새로운 주장, 연구자가 얻은 자료를 이용하여 입증하고자 하는 가설
-추정한 모평균이 새로운 것임을 주장하므로 지금까지 알려진 모수값과 차이가 있고, 이는 차이가 없다는 귀무가설에 ‘대립’되는 개념이다.
-귀무가설에 반하는 가설로서 가급적 입증하고 싶은 가설이다. 연구가설이라고도 한다. 대부분 새로운 것을 주장하는 것으로 실험이나 조사의 주된 목적이 된다. ① 귀무가설(
) : 지금까지 알려진 것과 같다. 검증의 대상이 된다
-표본에서 추정한 모평균이 지금까지 알려진 모수값과 같다는 주장을 하기 때문에 차이가 없다는 것을 강조하는 뜻에서 ‘귀무’라는 용어를 쓴다.
② 대립가설(
) : 새로운 주장, 연구자가 얻은 자료를 이용하여 입증하고자 하는 가설
-추정한 모평균이 새로운 것임을 주장하므로 지금까지 알려진 모수값과 차이가 있고, 이는 차이가 없다는 귀무가설에 ‘대립’되는 개념이다.
-귀무가설에 반하는 가설로서 가급적 입증하고 싶은 가설이다. 연구가설이라고도 한다. 대부분 새로운 것을 주장하는 것으로 실험이나 조사의 주된 목적이 된다.

나. 제Ⅰ종 오류와 제Ⅱ종 오류 : 잘못된 통계적 결론을 내리는 것
①제Ⅰ종 오류(typeⅠerror), α : 귀무가설이 맞는데 틀렸다고 결론을 내림으로써 틀린 대립가설을 채택했을 때 발생하는 오류이다. 맞는 귀무가설을 기각하는 경우에 발생하는 오류. (H0가 참인데H1 채택)
②제Ⅱ종 오류(typeⅡerror), β : 틀린 귀무가설을 맞다고 결정하여 생기는 오류이다. 귀무가설을 기각하지 못하는 경우에만 발생한다. ①제Ⅰ종 오류(typeⅠerror), α : 귀무가설이 맞는데 틀렸다고 결론을 내림으로써 틀린 대립가설을 채택했을 때 발생하는 오류이다. 맞는 귀무가설을 기각하는 경우에 발생하는 오류. (H1가 참인데H0 채택)


다. 유의수준 ( α: significance level ) : 가설검정에서 제Ⅰ종 오류가 발생할 확률의 최대 허용 한계
○ 귀무가설(영가설)이 사실일때 귀무가설을 기각할 오류의 최대 허용범위로써 5%정도는 우리가 잘못 판단할 수 있다고 감수한다는 뜻

마. 유의확률(p-value) : 내가 시행한 통계에서 귀무가설이 일어날 확률
○ 귀무가설이 옳은 경우에 검정통계량 값이 그 이상 극단적으로 나타날 확률 (※교재 p.199)
○ 유의수준 α 에서 p < α 이기만 하면 귀무가설은 기각된다.
- p값이 더 작으면 더 작은 유의수준에 대해서도 귀무가설을 기각할 수 있는 것은 사실이지만, 그 '정도'는 관계 없다
○ p=0.03의 해석
-“차이가 없다는 것이 사실 일 때, 표본에서 이것이 나타날 확률이 0.03밖에 되지 않는, 아주 드문 현상이 벌어진 것이다. 따라서 표본에서 이 만큼의 차이가 나타나는 이유는, 실제로 차이가 있기 때문이다‘
→ 차이가 있다는 주장에 대한 강한 증거
○ p=0.3의 해석
-“차이가 없다고 하더라도, 표본이 우연히 그 만큼의 차이를 보일 가능성이 흔하므로(30%), 차이가 있다는 충분한 근거가 되지 않는다”로 해석
9.2 가설검정 절차 : 가설설정→유의수준 결정→기각값 결정→검정통계량 계산→귀무가설 판정
| ① 귀무가설과 대립가설을 세운다. ② 유의수준(α )을 결정한다. ③ 기각값을 결정한다. 기각값은 귀무가설을 기각하는 기준값이다. ④ 검정통계량 값을 구한다. ⑤ 귀무가설의 채택 또는 기각 여부를 판정한다.검정통계량값이 기각값보다 클 때 귀무가설을 기각 ⑥ 가설검정 결과를 설명한다. |
가. 검정통계량과 기각값
○검정통계량(test statistics) : 귀무가설과 대립가설 중에 하나를 채택하는 데 쓰이는 통계량이다.
○기각값(critical value) : 귀무가설을 기각하는 기준이 되는 값으로 임계값이라고도 한다.
- 기각값은 유의수준에 따라 달라진다.
○정규분포(Z) : t–분포

○귀무가설의 채택․기각판정
•검정통계량값을 기각값과 비교하여 검정통계량값이 기각값보다 클 때 귀무가설을 기각하고, 기각값보다 더 작을 때 귀무가설을 채택하고, 한다.
•검정통계량값과 기각값은 +, - 부호에 관계없이 절대값으로 비교한다.


나. 기각역 vs. 채택역
○기각역(rejection region) : 기각값을 중심으로 귀무가설이 틀렸다고 기각하는 검정통계량의 영역
•기각값 바깥쪽 5% 지역이며, 표본평균이 이 지역에 위치하면 귀무가설을 기각한다. 기각값F > 검정통계량 FS
○채택역(acception region) : 귀무가설을 채택하는 영역
•기각값 안쪽 95% 지역으로 표본평균이 이 지역에 위치할 때 귀무가설을 채택한다.
○ 기각값은 (표준정규분포표 or t-분포표의) 표준화값으로 하든지 실제값으로 하든지 똑같은 결과를 얻게 된다. (※아래 예제). 실제 가설검정에서는 표준화값을 사용한다.

9.3 양측검정과 단측검정
| 가설검정에서 기각역을 표본분포의 양쪽에 설정하는 것을 양측검정(two-tailed test)라하고, 표본분포의 좌우 어느 한쪽에만 기각역을 설정하는 것을 단측검정(one-tailed test)이라 한다 |
가. 양측검정 : ‘추정한 모평균이 가정한 모수값과 차이가 없는지’를 검정하는 것이므로 귀무가설의 검정을 의미한다.
•양측검정은 추정된 모평균이 가정한 모수값과 ‘차이가 있는지 없는지(같은지 다른지)’를 검정하므로 기각역이 양쪽에 있다. 양측검정에서는 추정된 모평균이 가정한 모수값보다 크든 작든 관계없다.
• 따라서 귀무가설을 기각하면 “차이가 있다” 또는 “다르다”고만 말한다.




예9-4) t-분포에서 귀무가설의 채택역과 기각역 및 기각값
검정통계량값이(-3.594)는 기각값(-2.861)보다 작다. 표본평균(491)이 기각역의 실제값(492)보다 작다. 따라서 표본평균이 기각역에 있으므로 귀무가설 기각한다.
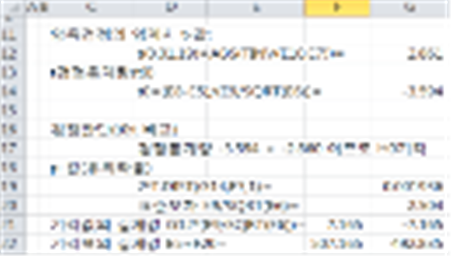
※예제 9-5 ) 단측검정
알 낳는 병아리는 보통사료로 사육하면 처음 6주 동안 체중이 450g으로 된다. 보통사료에 첨가제 B를 넣어 6주 사육한 후 10마리의 체중을 측정한 결과 평균이 500g이고 표준편차는 65g이었다. 이 첨가제는 체중을 증가시키는 데 효과가 있는가?

<풀이> ‘효과가 있는지’를 판정하는 것이므로 우측검정을 하는 단측검정이다
① 단측검정의 귀무가설과 대립가설을 세운다
𝐻0 : 𝜇 = 450, 평균체중은 450g과 차이가 없다.
𝑯𝟏 : 𝝁 > 450, 평균체중은 450g보다 더 크다.
② 유의수준은 𝛼=0.05로 정한다.
③ 기각값을 결정한다
모분산을 모르고 표본크기가 작으므로 𝒕 −분포를 이용한다.
또, 단측검정이므로
유의수준 𝜶 =𝟎.𝟎𝟓의 두배인 𝜶=𝟎.𝟎𝟓×𝟐=𝟎.𝟏를 찾는다.
𝑑𝑓=9 일 때 𝛼=0.05에서
=1.833
④ 검정통계량 ts의 값을 구한다.
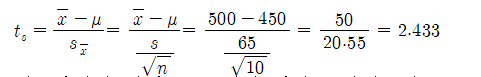
⑤ 귀무가설의 채택 또는 기각 여부를 판정한다.
𝒕𝒔 = 𝟐. 𝟒𝟑𝟑 > 𝒕0.1(0) = 𝟏.𝟖𝟑𝟑
𝑯𝟎: 𝝁 = 𝟒𝟓𝟎을 기각하고, 𝑯𝟏: 𝝁 > 𝟒𝟓𝟎을 채택한다.
⑥ 가설검정 결과의 설명
“첨가제 B는 체중증가에 유의한 효과가 있다.” 또는
“첨가제 B는 5% 유의수준에서 체중증가가 인정된다.”라고 결론 짓고, 𝒕𝒔 = 𝟐. 𝟒𝟑𝟑*로 나타낸다.
「정리하기」
1.가설검정은 모수값을 미리 가정해 놓고, 표본의 통계량이 가정한 모수와 어느 정도 일치 또는 불일치하는지를 검토하는 통계적 절차이다. 가설검정에 의해 귀무가설 또는 대립가설을 채택 또는 기각한다.
2.통계적 가설은 ‘지금까지 알려진 것과 같은’ 귀무가설(H0)과 ‘새롭게 주장하고자 하는’ 대립가설(H1)과 이 있으며, 가설검정의 절차는 ① 가설검정, ②유의수준 결정, ③ 기각값 결정, ④ 검정통계량값 계산, ⑤ 귀무가설의 채택 또는 기각 여부 판정, ⑥ 가설검정 결과 설명의 순서로 진행한다.
3.가설검정에서 제I종 오류(α)는 옳은 귀무가설을 기각하는 오류이고, 제II종 오류(β)는 틀린 귀무가설을 채택하는 오류이다. 가설검정의 검정력은 옳은 대립가설을 채택하는 확률(1-β)을 말하며, 오류를 줄이고 검정력을 크게 하려면 표본수를 늘려야 한다.
4.검정통계량은 귀무가설을 기각하거나 채택하는데 쓰이는 통계량으로 표본평균을 표준오차값으로 표준화시킨 것이며, 기각값은 귀무가설을 기각하는 기준이 되는 값이다.
5.양측검정은 기각역을 표본분포의 양족에 설정하고 가설검정을 하며, 단측검정은 기각역을 표본분포의 좌우 어느 한 쪽에만 설정하여 가설검정을 한다.
※ 부족하지만 글의 내용이 도움이 조금이라도 되셨다면, 단 1초만 부탁드려도 될까요? 로그인이 필요없는 하트♥(공감) 눌러서 블로그 운영에 힘을 부탁드립니다. 그럼 오늘도 행복한 하루 되십시오^^
'생물통계학' 카테고리의 다른 글
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 11. 여러 집단의 비교 (6) | 2022.11.22 |
|---|---|
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 10. 두 집단의 비교 (8) | 2022.11.18 |
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 8. 모수추정 (10) | 2022.11.16 |
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 7. 표본분포 (8) | 2022.11.15 |
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 6. 확률분포 (9) | 2022.11.14 |