11. 여러 집단의 비교
[학습개요]
하나 또는 두 개 모집단의 평균에 대한 검정에서 모분산을 알면
-검정을 하고, 모분산을 모르고 표본크기가 작을 때
-검정을 한다. 그리고 세 개 이상의 모집단을 동시에 비교하려면
-검정을 하는데, 이 방법은 집단 간의 분산과 집단 내의 분산을 이용하기 때문에 분산분석이라고 한다. 분산분석은 세 개 이상의 표본평균들이 같은 모집단에서 나온 것인지를 검정하며, 또한 실험에 관련된 요인들 가운데 가장 크게 영향을 끼치는 요인을 찾아내는 분석방법이다. 하나 또는 두 개 모집단의 평균에 대한 검정에서 모분산을 알면
-검정을 하고, 모분산을 모르고 표본크기가 작을 때
-검정을 한다. 그리고 세 개 이상의 모집단을 동시에 비교하려면
-검정을 하는데, 이 방법은 집단 간의 분산과 집단 내의 분산을 이용하기 때문에 분산분석이라고 한다. 분산분석은 세 개 이상의 표본평균들이 같은 모집단에서 나온 것인지를 검정하며, 또한 실험에 관련된 요인들 가운데 가장 크게 영향을 끼치는 요인을 찾아내는 분석방법이다.
| - T-검정은 두 집단간의 평균차이를 분석하고자 할 때 사용한다면, 분산분석은 세 개 이상의 집단 평균을 비교하기 위해 비교과정에 분산을 사용하는 통계적 기법이다. - 예컨대 세 개 이상의 집단평균이 같다는 가정은 분산이 동일하다는 가정이 내포된다. 따라서 분산분석은 각 집단의 분산을 분석하나 실제로는 각 집단의 평균이 동일하다는 가설을 검정하는 것이 된다. - 분산분석은 3개 이상의 표본들의 차이를 표본 평균간의 분산과 표본내의 관측치 간의 분산을 비교하여 가설을 검정하는 것이 주요내용이 된다. - 분산분석은 두 종류가 있다 ①일원분산분석(One-way ANOVA): 단 하나의 인자에 근거하여 여러 수준으로 나누어지는 분석 ②이원분산분석(Two-way ANOVA): 두개 이상의 인자에 근거하여 여러 수준으로 나누어지는 분석 - t-검정 : 두 집단의 평균간 차이를 비교할 때 - F-검정 : 세 개 이상의 여러 집단을 동시에 비교할 때 |
11.1. 분산분석의 개념
| F-검정을 하여 세 개 이상의 여러 집단을 동시에 비교하며, F-검정을 분산분석(analysis of variance, ANOVA)이라고 부른다 |
▪집단 간의 분산과 집단 내의 분산을 이용하므로 분산분석이라고 한다.
▪𝐹−검정은 𝐹−분포를 이용한다.
▪독립변수들의 수준을 조절한 다음 조절된 독립변수들의 각 수준 또는 둘 이상의 독립변수들의 수준 조합에 따라 제 각각 측정되는 하나 이상의 반응치에 대한 효과를 분석하는 연구
→실험 대상자들에게 서로 다른 처리를 가한 후에 그 결과를 관측하여 서로 다른 처리수준들 사이의 반응에 차이가 있는가를 분석하는 것
→ 서로 다른 3개 이상의 모집단에 있어서의 모평균이 동일한가를 검정하는 방법
가. 분산분석을 위한 가정
① (독립성)각 모집단 내에서의 오차나 모집단 간의 오차는 서로 독립이다.
•집단을 구성하는 개체들은 분석하는 변수와 관련된 요소들을 공유하지 않고 서로 독립적이어야 한다.
• 사료종류에 따른 돼지 증체효과를 분산분석 할 때 서로 다른 사료로 사육한 돼지는 서로 독립적이다.
② (정규성)각 집단에 해당되는 모집단의 분포가 정규분포이다.
• 종속변수는 정규분포를 해야 한다.
• 독립변수 : 사료종류
• 종속변수 : 체중 증가량 (분석변수)
③ (등분산성)각 집단에 해당되는 모집단의 분산은 서로 같다.
• 비교하는 모든 집단의 분산은 같아야 한다.
• 분산비(𝐹𝑠)와 𝐹−분포를 이용 분산의 동질성 검정
• 분산이 다를 때는 종속변수(𝑌)를

나.일원분산분석(one way ANOVA) : 반응치에 관여된 변수가 하나인 경우
| 예1)세탁물의 온도(A)에 따른 세탁된 결과를 정밀한 섬유측정기기로 점수화 한다. ① 미지근한 물 ②찬 물 ③ 더운 물 예2) 타이어의 종류가 갑, 을, 병 세 가지가 있을 때 타이어의 종류에 따라 주행거리가 차이가 있을 것인가를 검증한다고 하자. 이때 모집단은 세 개이며, 각각의 타이어에 대한 분산은 으로 모두 같다고 가정하자. 이때 사용되는 통계적인 검증방법으로 분산분석을 실시한다. 먼저, 분산분석을 실시하면 각 타이어(실험요인)에 대한 -값을 계산할 수 있다. 이 -값과 -분포표의 -값의 임계치와 비교하여 귀무가설을 채택할 것인지 기각할 것인지를 결정하게 된다. |
○ 가설설정
①귀무가설:

모든 평균은 다 같다.
모집단의 평균이 요인의 수준에 따라 차이가 없다는 것은, 한 변수가 다른 변수에 영향을 주지 못한다는 것과 동일한 의미이다.
②대립가설:
: 모든 평균( )이 모두 같지는 않다.
- 평균이 다른 집단이 적어도 하나 이상 있음.
②대립가설: H1: 모든 평균( )이 모두 같지는 않다.
- 평균이 다른 집단이 적어도 하나 이상 있음.
○ 데이터 구조
하나의 요인에 t종류의 처리가 있고 각 처리에 n개의 반복이 있는 경우를 반복수가 같은 일원배치법이라고 한다.
처리수준이 t이며, 반복수가 n으로 동일한 경우 분산분석의 자료형태는 아래의 표와 같다.


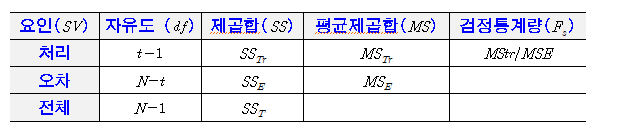
라. 분산분석표


마. 분산분석표에서 가설검정
위의 분산분석표에서 계산된 F값은 다음과 같은 가설검정에 이용된다. 이 때 귀무가설은 『각 처리간의 효과가 모두 동일하다』로, 대립가설은 『적어도 하나는 동일하지 않다』로 생각할 수 있다.


귀무가설
하에서 FS=MST/MSE는 자유도가 (t-1, t(n-1))인 F-분포를 따른다. 또한 귀무가설이 참인 경우에 FS값은 1에 가까워지는 반면 귀무가설이 참이 아닌 경우에 FS값은 1보다 크게 주어지므로 유의수준 a에서 기각역은 다음과 같이 주어진다.

2. 분산분석 절차
①가설을 설정한다.
②분산분석의 가정에 맞는지 확인한다.
③유의수준(α)을 결정한다.
④기각값( F값)을 결정한다.
⑤제곱합(ss)과 평균제곱합(MS)을 구한다.
⑥분산분석표를 작성하고 검정통계량(F2)의 값을 구한다.
⑦ F–검정에 의해 귀무가설의 채택 또는 기각 여부를 판정한다
⑧분산분석 결과를 설명한다.

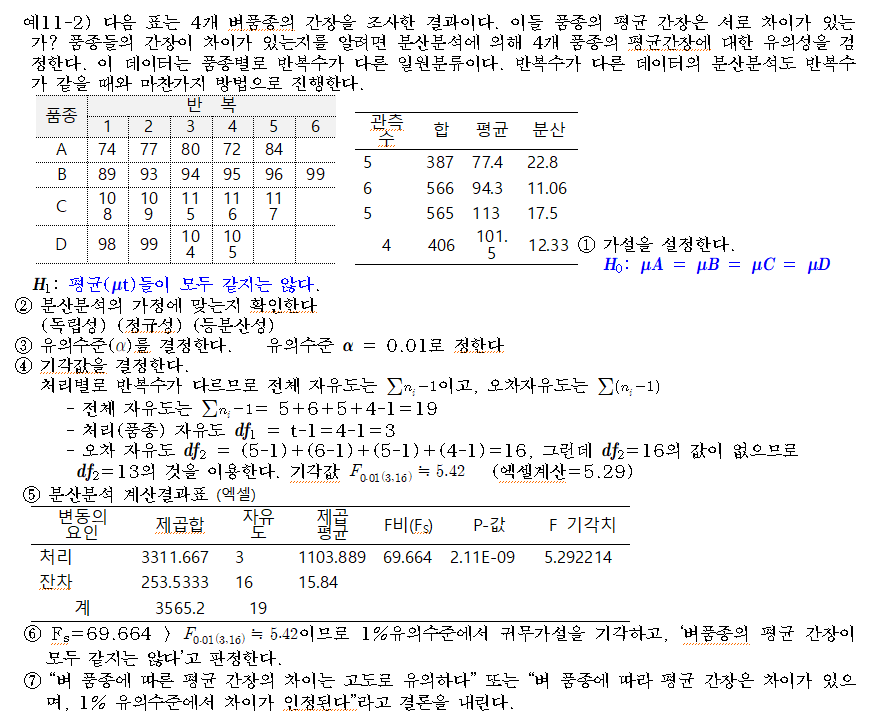
11.3. 반복수가 다른 일원분류의 데이터 분산분석 (반복수가 같지 않은 일원배치법)
○ 개념
실제의 일원배치법에서는 처리의 어떤 특정한 수준에 대하여 모평균추정의 정도(precision)를 높이기 위해 반복수를 다른 수준보다 많게 하거나, 측정에 실패하거나 결측치가 발생하여 처리에 따라 같은 수의 표본을 얻지 못하는 경우가 발생한다.
※ 일원배치법에서는 반복수가 다르더라도 특별한 수정 없이 그대로 분석할 수 있음
○ 반복수가 다른 경우 일원배치법의 통계적 모형은 다음과 같다.

○ 처리효과의 유의성 검정은 다음과 같이 요약될 수 있다.
<평균들의 동일성에 대한 F-검정)

「정리하기」

※ 부족하지만 글의 내용이 도움이 조금이라도 되셨다면, 단 1초만 부탁드려도 될까요? 로그인이 필요없는 하트♥(공감) 눌러서 블로그 운영에 힘을 부탁드립니다. 그럼 오늘도 행복한 하루 되십시오^^
'생물통계학' 카테고리의 다른 글
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 13. 상관분석(correlation analysis) (2) | 2022.11.24 |
|---|---|
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 12. 평균의 다중비교 (2) | 2022.11.23 |
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 10. 두 집단의 비교 (8) | 2022.11.18 |
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 9. 가설검정 (7) | 2022.11.17 |
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 8. 모수추정 (10) | 2022.11.16 |