제12장 평균의 다중비교
「학습개요」
여러 개의 평균을 비교하는 분산분석에서 유의성이 인정되면 그것은 두 개 이상의 평균이 같지 않다는 뜻이며, 그 결과가 어느 평균들 간에 유의한 차이가 있는지를 보여주지는 않는다. 따라서 여러 평균들 간의 차이를 동시에 비교하는 다중비교 방법을 사용한다. 생물학과 농학연구에서는 최소유의차(LSD)방법과 덩컨(Duncan)방법을 많이 사용한다.
「통계검정별 차이」
▪ 두 집단의 평균간 차이를 비교할 때 : 𝑡−검정
▪ 세 개 이상의 여러 집단을 동시에 비교할 때: 𝐹−검정
- 처리평균들 간의 유의성 여부만 검정
- 처리 평균들 간의 관계는 파악할 수 없음
▪ 처리평균의 다중비교
- 분산분석 결과를 통해 처리평균 간 유의성이 인정되어 귀무가설이 기각되고 대립가설이 채택된 경우에만 수행
12.1 평균 간 비교
| ○ 분산분석에서는 어느 평균이 어느 평균과 어떻게 차이가 나는지 알 수 없다. 따라서 분산분석 결과 평균들 간에 유의성이 인정되면, 그 다음 평균의 다중비교(multiple comparison)를 통해 어느 평균이 어느 평균과 차이가 있는지를 분석한다. - 분산분석 결과를 통해 처리평균 간 유의성이 인정되어 귀무가설이 기각되고 대립가설이 채택된 경우에만 수행한다 |
가. 평균 간 비교의 다양성
○ 평균들은 여러 가지로 비교할 수 있으나, 실험목적에 부합되는 비교를 하는 것이 중요하다.
- 예를 들어 논에서 4개 처리의 손제초와 10개 처리의 약제초, 1개의 대조구(모두 15개 처리구)로 제초방법에 관한 실험을 했을 때, 여러 가지 비교 방법을 생각해 볼 수 있다.
| 다중비교는 자료수집 이전에 계획된 계획비교(사전비교)와 귀무가설이 기각된 후 새로운 사실을 찾아내기 위하여 실시하는 사후비교로 구분할 수 있다. 사전비교는 모든 집단의 평균이 같으냐의 여부보다는 특정 집단간의 평균의 차이를 규명하는 것이 주목적이다. 따라서 사전에 염두에 둔 특정 집단간의 평균의 차이가 유의적인가에 대한 가설검증이 주목적이므로 분산분석에서의 가설검증에는 관심의 대상이 아니라고 할 수 있다. 그러나 사후분석은 모든 집단의 평균이 같은 가에 대한 관심이 우선하므로 영가설을 기각한 후 어떤 집단간의 평균이 다른가에 규명하여 영가설을 기각한 이유를 규명하는 것이 주목적이라고 할 수 있다. |
① 계획된 비교
○실험 전 미리 비교의 짝을 정하는 것으로, 여러 처리의 각각을 대조(control, check) 비교하는 것으로
최소유의차(LSD)검정이 해당된다
② 비계획된 비교
○실험결과를 보고 비교 짝을 만들거나, 처리 간에 모든 가능한 비교를 하는 것으로
덩컨(duncan)의 다중범위검정이 해당된다
나. 평균의 다중비교
○다중비교의 원리는 여러 개 평균을 반복해서 비교하더라도
전체적인 제Ⅰ종 오류의 크기 α(예를 들면 α=0.05)를 넘지 않도록 하는 것이다.
○다중비교 방법: 최소유의차(LSD)방법, 덩컨(Duncan)방법, 투키(Tukey)방법, 슈페(Scheffé)방법, 본페로니(Bonferroni)방법, 던네트(Dunnett)방법, 스튜던트–뉴맨–컬(Student–Newman–Keul)방법이 있다.
| (사례) 제초방법을 비교하는 실험 방법 : 손제초(4가지), 제초제 사용(10가지) (연구)▪ 제초효과가 있는 처리는 어느 것인가? ▪ 14개 제초방법 간에 차이가 있는가? 있다면 효과 있는 처리와 효과 없는 처리는 어느 것인가? ▪ 손제초와 제초제 처리 간에는 차이가 있는가? ▪ 4개 손제초 방법 간에 차이가 있는가? 차이가 있다면 어느 방법이 가장 좋은가? ▪ 10개 제초제 처리 간에 차이가 있는가? 차이가 있다면 어느 처리가 가장 좋은가? |
12.2 최소유의차방법
가. 최소유의차(least significant difference, LSD)
○ 최소유의차(LSD)값을 기준으로 사용하여 평균들의 가능한 모든 짝비교를 하는 방법이다. 평균의 짝비교는 두 평균의 가능한 모든 차이를 비교하는 것이다. 두 모집단 평균차이 검정에서 통합분산(pooled variance) 대신에 MSE(평균 오차 자승합) 사용한다.
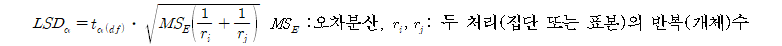
두 평균이 a에서 유의적 차이를 보이려면 적어도 LSD평균 차이 이상 커야한다.

12.3. 덩컨(Duncan)방법
○ 덩컨방법은 비교하는 평균수에 관계없이 결정한 유의수준(a)을 유지하면서 모든 평균 간의 비교를 하며, 이를 덩컨의 다중범위검정(Duncan’s multiple range test, DMRT)이라 한다.
가. 최소유의범위
○덩컨의 다중범위검정은 평균을 크기순으로 나열하고, 비교하는 두 평균의 가깝고 먼 위치에 따라 다른 기준값을 적용한다. 그 기준값을 최소유의범위(least significant range)라 한다.
- 표본의 평균을 크기 순서에 따라 다수의 범위를 이용하여 신뢰구간을 구하여 모집단 평균간의 차이에 대한 검증만을 할수 있는 절차이기 때문에 다중범위검증(Multiple Range Tests)이라고 불리어진다.
나. 평균의 다중비교
○ 다중범위검증에서는 먼저 표본평균을 크기순서로 놓고 r개의 평균 중에서 p개의 평균을 선택하여 크기순서로 배열한다. p개의 평균 중에서 최대값과 최소값의 차이가 아래의 임계값보다 크면 유의수준
에서 차이가 있다고 할 수 있고, 작으면 차이가 없다고 할 수 있다. ○ 덩컨방법은 비교하는 평균수에 관계없이 결정한 유의수준(
)을 유지하면서 모든 평균 간의 비교를 하며, 이를 덩컨의 다중범위검정(Duncan’s multiple range test, DMRT)이라 한다.
가. 최소유의범위
○덩컨의 다중범위검정은 평균을 크기순으로 나열하고, 비교하는 두 평균의 가깝고 먼 위치에 따라 다른 기준값을 적용한다. 그 기준값을 최소유의범위(least significant range,
)라 한다.
- 표본의 평균을 크기 순서에 따라 다수의 범위를 이용하여 신뢰구간을 구하여 모집단 평균간의 차이에 대한 검증만을 할수 있는 절차이기 때문에 다중범위검증(Multiple Range Tests)이라고 불리어진다.
나. 평균의 다중비교
○ 다중범위검증에서는 먼저 표본평균을 크기순서로 놓고 r개의 평균 중에서 p개의 평균을 선택하여 크기순서로 배열한다. p개의 평균 중에서 최대값과 최소값의 차이가 아래의 임계값보다 크면 유의수준
에서 차이가 있다고 할 수 있고, 작으면 차이가 없다고 할 수 있다. 가. 최소유의범위
○덩컨의 다중범위검정은 평균을 크기순으로 나열하고, 비교하는 두 평균의 가깝고 먼 위치에 따라 다른 기준값을 적용한다. 그 기준값을 최소유의범위(least significant range,
)라 한다.
- 표본의 평균을 크기 순서에 따라 다수의 범위를 이용하여 신뢰구간을 구하여 모집단 평균간의 차이에 대한 검증만을 할수 있는 절차이기 때문에 다중범위검증(Multiple Range Tests)이라고 불리어진다.
나. 평균의 다중비교
○ 다중범위검증에서는 먼저 표본평균을 크기순서로 놓고 r개의 평균 중에서 p개의 평균을 선택하여 크기순서로 배열한다. p개의 평균 중에서 최대값과 최소값의 차이가 아래의 임계값보다 크면 유의수준
에서 차이가 있다고 할 수 있고, 작으면 차이가 없다고 할 수 있다.

따라서 이 검증은 선택한 p개의 부분집합이 같은 부류의 집단인지 아닌지를 판명하는데 사용하고 있다.
○ Duncan방식은 비교하려고 선택한 부분집합의 집단의 수를 사용하고 있으며
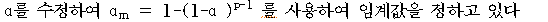
<예12-2) 5가지 사료의 돼지 증체량에 대한 5반복 실험의 평균 증체량 분산분석 결과가 아래와 같을 때, 5 가지 사료간의 증체효과에 대해 비교하라.
①덩컨방법을 사용해도 좋은지 판단한다.
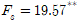
②평균을 크기순으로 정리한다.
③유의수준(𝛼)을 결정한다.
a=0.05
④ 표준오차를 구한다
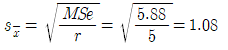
⑤ 𝑆𝑆𝑅 값을 구한다
분산분석표의 오차자유도 𝒅𝒇 = 𝟐𝟎이므로 <부표 9,다중검정을 위한 스튜던트화한 범위>로 부터 𝒅𝒇 = 𝟐𝟎에서 𝜶 = 𝟎. 𝟎𝟓 일 때 𝒑 = 𝟐부터 𝒑 = 𝟓 까지 𝑺𝑺𝑹값을 구한다..
⑥ 최소유의범위 (LSR) 값을 구한다.
⑦다중비교에 의한 평균 간 차이의 유의성 검정
㉠가장 큰 평균과 가장 큰 LSR값에 의한 비교

㉠가장 큰 평균과 가장 큰 LSR값에 의한 비교

㉡두 번째 큰 평균과 두 번째 큰 LSR값에 의한 비교
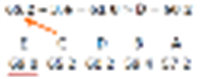
㉢세 번째 큰 평균과 세 번째 큰 LSR값에 의한 비교
㉣계속적인 비교
⑧다중비교 결과를 밑선이나 문자로 나타낸다.
사용된 밑선 수가 3개이므로 문자도 3개를 사용한다.
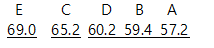
문자 표시

⑨ 덩컨의 다중범위검정 결과 설명
㉠5가지 사료의 돼지 증체효과는 (A, B, D), C, E 등 세 그룹으로 나눌 수 있으며, 각 그룹 간 평균 증체량의 차이는 5% 유의수준에서 차이가 인정되었다.
㉡사료의 증체효과는 사료 E가 가장 컸고 사료 A가 제일 낮았다.
㉢사료 A, B, D의 증체효과는 같은 것으로 나타났다.

(질문)
㉠오차의 자유도는 얼마인가?
㉡전체 𝑆𝑆는 얼마인가?
㉢처리 𝑀𝑆와 오차 𝑀𝑆는 얼마인가?
㉣Fs값을 구하고 1% 유의수준에서 F-검정을 하라.
㉤ F-검정의 결과를 해석하라. 처리평균들 간에 유의한 차이가 있다
㉥이 실험의 실험단위는 총 몇 개인가? 20
㉦ 이 실험의 처리수는 몇 개인가? 4
㉧이 실험의 반복수는 몇 개인가? 5
「정리하기」
1.분산분석 결과 유의성이 인정되면 평균의 다중비교에 의해 평균 간 차이의 유의성 여부를 검정하며, 최소유의차검정과 덩컨의 다중검정을 주로 사용한다.
2.최소유의차검정은 계획된 비교에 적합하며 평균수 4개까지만 비교하는 것이 적당하며, 덩컨의 다중범위검정은 결정한 유의수준을 유지하면서 평균수에 관계없이 가능한 모든 평균 간 비교를 할 수 있으며, 비계획된 비교방법으로 많이 사용된다.
3.덩컨의 다중범위검정은 먼저 처리평균을 크기순으로 나열하고 처리평균의 표준오차를 구한 다음, SSR값을 찾아 LSR값을 구한다. 평균의 다중비교는 평균간 차이와 LSR 값을 비교하여, 유의성이 없는 평균들은 밑선으로 연결하거나 같은 문자로 표시한다.
※ 부족하지만 글의 내용이 도움이 조금이라도 되셨다면, 단 1초만 부탁드려도 될까요? 로그인이 필요없는 하트♥(공감) 눌러서 블로그 운영에 힘을 부탁드립니다. 그럼 오늘도 행복한 하루 되십시오^^
'생물통계학' 카테고리의 다른 글
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 14. 회귀분석(regression analysis) (2) | 2022.11.25 |
|---|---|
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 13. 상관분석(correlation analysis) (2) | 2022.11.24 |
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 11. 여러 집단의 비교 (6) | 2022.11.22 |
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 10. 두 집단의 비교 (8) | 2022.11.18 |
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 9. 가설검정 (7) | 2022.11.17 |