제13장 상관분석(correlation analysis)
[학습개요]
1.같은 실험단위에서 관찰한 두 변수 사이에 원인과 결과의 관계가 있으면 회귀방정식을 구하여 그 인과관계를 설명하고, 한 변수의 변화에 따른 다른 변수의 변화를 예측할 수 있다. 이 때 두 변수 사이의 관계가 얼마나 강한지, 또 회귀방정식이 얼마나 정확하게 예측할 수 있는지 상관분석을 통해 확인할 수 있다. 상관분석은 두 변수의 공분산으로부터 상관계수를 구하고 유의성을 검정하며, 상관계수는 단위가 없어 두 변수 사이에 상관 정도만을 나타낸다.
2.두 개의 연속형 변수가 있을 때 이들 간의 관련된 정도를 알아보는 방법을 상관분석이라고 한다. 상관관계는 두 변수가 함께 변화하는 직선적 관계를 뜻하며 상관계수(correlation coefficient) ‘r’을 구하여 상관정도를 나타낸다. 상관관계가 클수록 두 변수 사이에 직선적 관계가 강하다는 것을 의미한다.
상관분석은 상관계수를 구하고, 모상관계수의 유의성 검정 및 결정계수를 구함으로써 변수들 사이의 상관관계를 분석한다.
(개념) ‧하나의 변수가 다른 변수와 어느 정도 밀접한 관련성을 갖고 변화하는 가를 알아보기위해 사용
(ex) 소득과 소비성향, 쇼핑시간과 구매액
(원리) ‧관련성의 정도는 독립변수의 분산(소비액의 변화)중에서 다른 변수(소득의 변화)와 같이 변화하는 분산(공분산)이 어느 정도 되느냐
‧[-1≤상관계수(r)≤1]사이의 값을 가지며, 절대값 1에 가까울수록 상관성이 높다.
‧음(-)과 양(+)은 두 변수 관계의 방향성을 의미한다
(두 변수의 관계) : 일반적으로 선형관계에 초점을 두고 두 변수가‧선형관계를 갖는지
‧선형관계를 갖는다면 어느 방향인지:음(-) 또는 양(+)
‧그 관계는 얼마나 큰지를 분석 : [-1~1, 무상관=0]
[상관과 회귀]
관련있는 두 변수의 관계를 규명하는 분석으로 두 변수의 관련성을 눈으로 확인하는 산점도의 작성, 하나의 수치로 관련성의 방향과 강도를 파악하기 위한 상관계수의 산출, 두변수 간의 관련성을 하나의 함수식으로 찾아보는 회귀식의 적합과 유의성 검정을 다룬다.
▪산점도(scatter diagram) : 서로 대응되는 두 개의 짝으로 된 데이터를 좌표 평면상에 점으로 나타낸 그림(xi, yj)
▪상관분석(correlation analysis)
- 비교하는 두 변수가 모두 독립변수이다.
-두 변수 사이에 서로 유의한 관계가 있을 때 상관관계(correlation)이 있다고 말한다.
-동일한 실험단위에서 측정된 두 독립변수 간의 공분산을 계산하여 상관계수를 추정하고 모상관계수의 유의성을 검정하는 통계적 방법
▪회귀분석(regression analysis)
-독립변수와 종속변수가 존재한다.
-변수들 간에 원인과 결과의 관계를 나타낸다.
14.1 상관계수(correlation coefficient, r) : 상관계수를 통해 두 변수의 상관관계가 얼마나 강한가를 알 수 있다.
▪ 𝒓 = 𝟎은 두 변수 사이에 직선적 상관관계가 없음을 의미하며, 0 상관(zero correlation) 또는 무상관(no correlation)이라고 한다.
▪ 𝒓 = 𝟎 이 두 변수 간에 직선적 관계가 없다는 의미이며, 두 변수 사이에 아무런 관계가 없다는 의미는 아니다.


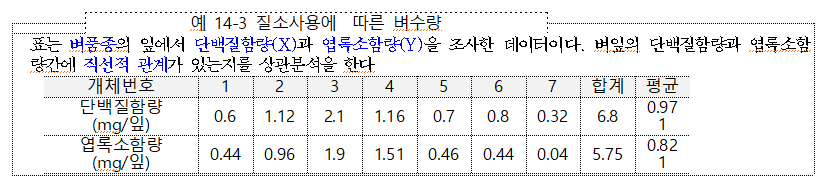
상관계수 구하기
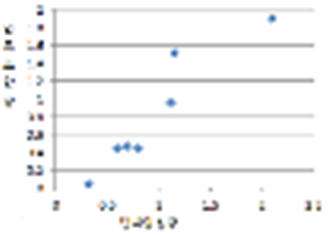
○ 산점도를 그려서 두 변수 관계 알아본다
- 위 산점도 그림은 단백질함량과 엽록소 함량간에 직선적 관계가 있음을 알수 있다.
○ 상관계수를 구한다
- 상관계수는 다음과 같이 구해진다.

14.2 상관계수 검정
상관계수의 검정
○ 검정통계량
• 상관계수 𝑟 이 +1이나 -1에 가까우면 검정통계량
의 값은 커지고, 𝑟 이 0에 가까울수록
값도 0에 가까워진다.
• 따라서
값이 0에 가까우면 모상관계수 𝜌 = 0이라는 귀무가설이 맞다는 뜻이므로 귀무가설을 채택한다.
○ 가설 설정
• 상관계수의 가설검정은 표본상관계수 r을 이용하여 모상관계수𝜌 를 검정하는 것이다.

○ 유의성 검정 (t-분포 또는 부표8(상관계수의 유의성 검정))
• 𝒕𝒔 > 𝒕𝟎.𝟎𝟓(𝒏−𝟐) 또는 𝒕𝒔 > 𝒕𝟎.𝟎𝟏(𝒏−𝟐) 일 때, 귀무가설 𝐻0 : 𝜌 = 0 을 기각한다.
• 귀무가설이 기각되면 상관계수는 유의한 것이 되고, 이는 상관계수가 두 변수의 직선관계를 잘 설명한다는 의미이다.
• 상관계수가 높더라도 유의성이 인정되지 않으면 그 상관계수는 의미가 없다.
① 방법 t-분포 이용
- 표본상관계수 r을 변환한 통계량의 분포는 자유도
V=n-2인 t-분포를 따른다.

② 방법 <부표 8 상관계수의 유의성 검정값> 이용
- <부표8>에서 자유도=n-2=7-2=5일 때 유의성 검정값 1% 유의수준에서(α=0.01)에서 0.874이다. 계산된 상관계수 r=0.942는 검정값 0.874보다 크므로 귀무가설을 기각하고 상관계수는 1% 유의수준에서 유의하다고 판정한다.
상관분석 설명
○ 상관계수와 결정계수를 제시하고 상관분석 결과를 설명한다.

※ 상관계수와 회귀계수의 관계
○ 상관계수와 회귀계수는 서로 밀접한 관계가 있다.
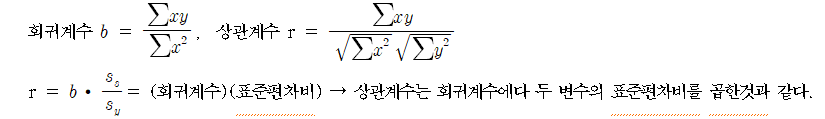
- 만약 두 변수의 표준편차가 동일하면 b=r로서 회귀계수와 상관계수는 똑같은 값을 가진다.
○ 상관계수가 0일 때 두 변수 간에 단지 직선적 관계가 없다는 뜻이며,
두 변수 사이에 관계가 전혀 없다는 의미는 아니다. 두 변수간에 직선적 관계가 없어도 곡선의 관계는 얼마든지 있을 수 있다 .
「정리하기」

※ 부족하지만 글의 내용이 도움이 조금이라도 되셨다면, 단 1초만 부탁드려도 될까요? 로그인이 필요없는 하트♥(공감) 눌러서 블로그 운영에 힘을 부탁드립니다. 그럼 오늘도 행복한 하루 되십시오^^
'생물통계학' 카테고리의 다른 글
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 15. 교차분석 (5) | 2022.11.29 |
|---|---|
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 14. 회귀분석(regression analysis) (2) | 2022.11.25 |
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 12. 평균의 다중비교 (2) | 2022.11.23 |
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 11. 여러 집단의 비교 (6) | 2022.11.22 |
| 농업직 연구사 공무원, 생물학 등 생물통계학 핵심 요점 정리 10. 두 집단의 비교 (8) | 2022.11.18 |